Fundamentals of Convective Heat Transfer

Week-12 (Live Session)

Durga Prasad Pydi

2025-10-11

Table of contents

• Introduction
• Pool Boiling Curve
• Laminar film condensation on a vertical plate
• Problems
  • Bubble radius
  • Heat Transfer Rate - Steam Relief Valve in pressurised cylinder
  • Condensation Rate - Vertical vs Inclined Plates
  • Condensation Rate - Vertical Plate vs Horizontal Cylinder
  • Condensation Rate - Flat vs Round Tube cross-section

Introduction

Evaporation	Boiling
Surface phenomenon	Bulk Phenomenon
$P_{v}<P_{sat}$ at a given $T$	$T_{w}>T_{sat}$
No bubbles observed	Usually accompanies by bubbles

$Nu=f\left( Gr=\frac{\rho g (\rho_{l}-\rho_{v})L^{3}}{\mu^{2}},Ja=\frac{c_{p}(T_{w}-T_{sat})}{h_{fg}},Pr=\frac{\mu c_{p}}{\kappa},Bo=\frac{g (\rho_{l}-\rho_{v})L^{2}}{\sigma^{2}} \right)$

where $Nu\to \text{Nusselt number}, Gr\to \text{Grashof number}$ $Ja\to \text{Jakob number}, Pr\to \text{Prandtl number}, Bo\to \text{Bond number}$

	Pool Boiling	Flow Boiling
Cause for fluid motion	natural convection	external means

Subcooled boiling	Saturated Boiling
$T_{l}<T_{sat}$	$T_{l}>T_{sat}$

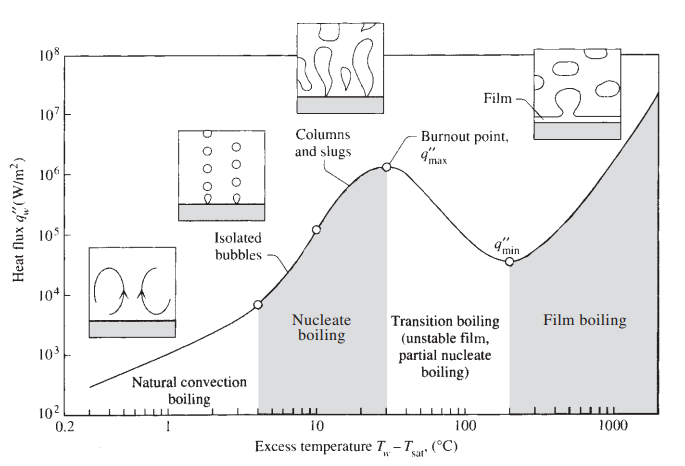
Pool Boiling Curve

Figure 1: Regimes of pool boiling in water at atmospheric pressure

Laminar film condensation on a vertical plate

liquid film thickness, $\delta(x)=\left(\frac{4 \mu_{l}\kappa_{l}(T_{sat}-T_{w})x}{h_{fg}' g \rho_{l}(\rho_{l}-\rho_{v})}\right)^{1/4}$

liquid film velocity, $u(x,y)=\frac{g(\rho_{l}-\rho_{v})\delta^{2}}{\mu_{l}} \left[\frac{y}{\delta}-\frac{1}{2} (\frac{y}{\delta})^{2}\right]$

liquid mass flow rate per unit width, $\dot{m}=\frac{g \rho_{l}(\rho_{l}-\rho_{v})\delta^{3}}{3\mu_{l}}$

liquid film temperature, $\frac{T_{sat}-T(x,y)}{T_{sat}-T_{w}}=1-\frac{y}{\delta}$

Local Nusselt number:

$$Nu = \left[ \frac{h_{fg}' g \rho_{l}(\rho_{l}-\rho_{v})x^{3}}{4 \mu_{l}\kappa_{l}(T_{sat}-T_{w})} \right]^{1/4}$$ where $h_{fg}'=h_{fg}(1+0.68 Ja)$

Mean Nusselt number:

$$\overline{Nu} = \frac{4}{3} \left. Nu\right|_{x=L}$$

Problems

Bubble radius

Consider the spherical vapor bubble of radius r shown in figure. The pressure and temperature inside the bubble $(P_{v},T_{v})$ are slightly above the pressure and temperature in the liquid $()P_{l},T_{l})$. The liquid is saturated, $T_{l}=T_{sat}$.

1. Invoke the mechanical equilibrium of one hemispherical control volume and derive the relation between bubble radius and pressure difference.

2. Rely on the Clausius–Clapeyron thermodynamics relation $\frac{dP}{dT}=\frac{h_{fg}}{T v_{fg}}$ and express the above equation in terms of temperature difference of vapor and saturation temperature.

3. Calculate the radius of a steam bubble with $T_{v}-T_{sat}=2K$ in water at$T_{sat}=100^{0}C$. (Take $\sigma=0.0589 N / m$, $h_{fg}=2257 kJ / kg$, $v_{g}=1.673 m^{3} / kg$)

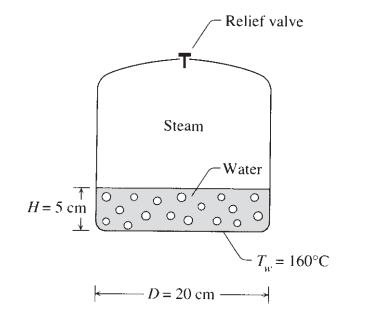
Heat Transfer Rate - Steam Relief Valve in pressurised cylinder

Water boils in the pressurized cylindrical vessel shown below. The steam relief valve is set in such a way that the pressure inside the vessel is 4.76 bar. The bottom surface is made out of copper (polished), and its temperature is maintained at Tw = 160⁰C. Assume nucleate boiling, and calculate the total heat transfer rate from the bottom surface to the boiling water. Later, verify the correctness of the nucleate boiling assumption.

$$q_{w}''=\mu_{l}h_{fg}\left[ \frac{g(\rho_{l}-\rho_{v})}{\sigma} \right]^{1/2}\left( \frac{c_{p,l}\Delta T_{e}}{C_{s,f}h_{fg}Pr_{l}^{n}} \right)^{3}$$

Take all property values for water and steam at 4.76 bar saturation pressure

$T_{sat}=15 0^{0}C$
$\rho_{l}=917.07 kg / m^{3}$	$c_{p,l}=4310 J / kg.K$
$\rho_{v}=2.548 kg / m^{3}$	$h_{fg}=2113.67 kJ / kg$
$\mu_{l}=1.81 \times 10^{-4} Pa.s$	$Pr_{l}=1.14$	$\sigma=0.0488 N / m$
$C_{s,f}=0.0128$	$n=1$

Condensation Rate - Vertical vs Inclined Plates

A plane rectangular surface of width $L=1m$ and temperature $T_{w}=80^{0}C$ is suspended in saturated steam of temperature $100^{0}C$. When this surface is oriented such that $L$ is aligned with the vertical, the steam condenses on it at the rate of $0.063 kg /s .m$. Calculate the condensation rate when the $L$ width makes an angle $45^{0}$ angle with the vertical. Determine also the film Reynolds number and the flow regime.

Condensation Rate - Vertical Plate vs Horizontal Cylinder

Saturated vapor condenses on a cold vertical slab of height L. Both sides of the slab are covered by laminar films of condensate. A single horizontal cylinder of diameter D and at the same temperature as the slab is immersed in the same saturated vapor. For what special diameter D will the total condensation rate on the cylinder equal the total condensation rate produced by the slab?

Condensation Rate - Flat vs Round Tube cross-section

The horizontal thin-walled tube shown in the figure is cooled by an internal fluid of temperature $T_{w}$. The tube is immersed in a stagnant atmosphere of saturated vapor, which condenses in laminar-film fashion on the outer cylindrical surface. It is proposed to increase the total condensation rate by flattening the tube cross section into the shape shown on the right side of the figure. Calculate the percent increase in condensation flow rate associated with this design change.

Thank You

Go to Home