Fundamentals of Convective Heat Transfer

Week-09 (Live Session)

Durga Prasad Pydi

2025-09-20

Assumptions

  • Steady, laminar, 2D flow
  • Viscous dissipation term is neglected
  • Boundary layer approximation is valid (δT/H≪1\delta_T/H \ll 1)
  • Temperature difference between plate and flud is small enough to assume constant properties of the fluid
  • Flow is incompressible - however, density will vary with location. The assumption is valid because the change in density is due to changes in temperature field
Figure 1: Illustration of natural convection over a vertical heated plate

Integral equations

Momentum Integral Equation

ddy∫0δρv2dx=−μ∂v∂x|x=0+∫0δρgβ(T−T∞)dx \frac{d}{dy} \int_{0}^{\delta} \rho v^{2} dx = -\mu \left.\frac{ \partial v }{ \partial x } \right|_{x=0} + \int_{0}^{\delta}\rho g \beta (T-T_{\infty}) dx

Energy Integral Equation

ddy∫0δT≈δv(T−T∞)dx=−α∂T∂x|x=0 \frac{d}{dy} \int_{0}^{\delta_{T} \approx \delta} v (T-T_{\infty})dx = -\alpha \left. \frac{ \partial T }{ \partial x } \right|_{x=0}

Approximating velocity and temperature with, vv0=xδ(1−xδ)2\frac{v}{v_{0}}=\frac{x}{\delta}\left( 1-\frac{x}{\delta} \right)^{2} and T−T∞Tw−T∞=(1−xδ)2\frac{T-T_{\infty}}{T_{w}-T_{\infty}}=\left( 1-\frac{x}{\delta} \right)^{2}, and solving for δ,v\delta, v from integral equations, we obtain,

v0=5.17νy(Pr+2021)−1/2Gry1/2 v_{0}=5.17 \frac{\nu}{y} (Pr+\frac{20}{21})^{-1/2}Gr_{y}^{1/2}

and

h(y)=2κy13.93(20211Pr+1)−1/4Ray1/4Nulocal=0.508(20211Pr+1)−1/4Ray1/4 \begin{align} h(y) & =\frac{2\kappa}{y} \frac{1}{3.93} (\frac{20}{21} \frac{1}{Pr} +1)^{-1/4}Ra_{y}^{1/4} \\ Nu_{local} & =0.508 \left( \frac{20}{21} \frac{1}{Pr} +1 \right)^{-1/4} Ra_{y}^{1/4} \end{align}

and Nu¯=43Nulocal\overline{Nu}=\frac{4}{3} Nu_{local}

Correlations - Vertical Plates

Geometry LcL_{c} Range of RaRa NuNu
LL 104−10910^{4}-10^{9}

1010−101310^{10}-10^{13}

Entire Range		 Nu=0.59RaL1/4Nu=0.59 Ra_{L}^{1/4}

Nu=0.1RaL1/3Nu = 0.1 Ra_{L}^{1/3}

Nu=(0.825+0.387RaL1/6(1+(0.492Pr)9/16)8/27)2Nu = \left(0.825 + \frac{0.387Ra_{L}^{1/6}}{\left( 1+\left( \frac{0.492}{Pr} \right)^{9/16} \right)^{8/27}}\right)^{2}
LL Use vertical plate equations for the upper surface of a cold plate and lower surface of a hot plate

Replace gg by gcosθg \cos \theta for −600≤θ≤600-60^{0}\leq\theta \leq 60^{0}

Correlations - Horizontal Plates

Geometry LcL_{c} Range of RaRa NuNu
Ap\frac{A}{p} 104−10710^{4}-10^{7}

107−101110^{7}-10^{11}		 Nu=0.59RaL1/4Nu = 0.59Ra_{L}^{1/4}

Nu=0.1RaL1/3Nu = 0.1 Ra_{L}^{1/3}
Ap\frac{A}{p} 105−101110^{5}-10^{11} Nu=0.27RaL1/4Nu = 0.27 Ra_{L}^{1/4}

Correlations - Cylinders

Geometry LcL_{c} Range of RaRa NuNu
LL A vertical cylinder can be treated as a vertical plate when D≥35LGrL1/4D\geq \frac{35L}{Gr_{L}^{1/4}}
DD RaD≤1012Ra_{D}\leq 10^{12} Nu=(0.6+0.387RaD1/6(1+(0.559Pr)9/16)8/27)2Nu = \left(0.6+\frac{0.387Ra_{D}^{1/6}}{\left( 1+\left( \frac{0.559}{Pr} \right)^{9/16} \right)^{8/27}}\right)^{2}

Correlations - Sphere

Geometry LcL_{c} Range of RaRa NuNu
DD RaD≤1011Ra_{D}\leq 10^{11}, Pr≥0.7Pr \geq 0.7 Nu=2+0.589RaD1/4(1+(0.469Pr)9/16)4/9Nu = 2+\frac{0.589Ra_{D}^{1/4}}{\left( 1+\left( \frac{0.469}{Pr} \right)^{9/16} \right)^{4/9}}

Correlations - Mixed Convection

Figure 2: Regimes of free, forced, and mixed-convection flow through horizontal circular ducts with UWT boundary condition - From Metais, B. and Eckert, E. R. G., J. Heat Transfer, 86C, 295, 1964.

Correlations - Between Parallel Walls

θ\theta Range of RaRa NuNu
90090^{0} 4×104−1084\times 10^{4} - 10^{8} 0.28Ra1/4(HL)−1/40.28 Ra^{1/4}\left( \frac{H}{L} \right)^{-1/4}
000^{0} 5×108−7.97×1085\times 10^{8}-7.97 \times 10^{8} 0.069Ra1/3Pr0.0740.069 Ra^{1/3}Pr^{0.074}
30030^{0} 5×108−7.97×1085\times 10^{8}-7.97 \times 10^{8} 0.065Ra1/3Pr0.0740.065 Ra^{1/3}Pr^{0.074}
45045^{0} 5×108−7.97×1085\times 10^{8}-7.97 \times 10^{8} 0.059Ra1/3Pr0.0740.059 Ra^{1/3}Pr^{0.074}
60060^{0} 5×108−7.97×1085\times 10^{8}-7.97 \times 10^{8} 0.057Ra1/3Pr0.0740.057 Ra^{1/3}Pr^{0.074}
90090^{0} 5×108−7.97×1085\times 10^{8}-7.97 \times 10^{8} 0.049Ra1/3Pr0.0740.049 Ra^{1/3}Pr^{0.074}

For air the simplified correlations are given below

NuL=0.18GrL1/4(HL)−1/92×103<GrL<2×104NuL=0.65GrL1/3(HL)−1/92×104<GrL<11×106 \begin{align} Nu_{L} & = 0.18 Gr_{L}^{1/4} \left( \frac{H}{L} \right)^{-1/9} & & 2\times 10^{3} < Gr_{L} < 2 \times 10^{4} \\ Nu_{L} & =0.65 Gr_{L}^{1/3} \left( \frac{H}{L} \right)^{-1/9} & & 2 \times 10^{4} < Gr_{L} < 11\times 10^{6} \end{align}

Problems

Integral Solution for Uniform Heat Flux

Determine the local Nusselt number for the boundary layer natural convection along a q″=constantq''=\text{constant} vertical wall by performing an integral analysis using the profiles

T−T∞=ΔT(1−xδT)2,v=Vxδ(1−xδ)2 \begin{align} T-T_{\infty}=\Delta T\left( 1-\frac{x}{\delta_{T}} \right)^{2}, & & v=V \frac{x}{\delta}\left( 1-\frac{x}{\delta} \right)^{2} \end{align}

and taking δ=δT\delta=\delta_{T}. Determine the expression for wall temperature profile.

Solution

Integral Solution in Stratified Ambient

Consider the integral analysis of laminar natural convection along a vertical wall bathed by a linearly stratified fluid as shown alongside. Starting with equations below,

ddy(∫0δ(y)v2dx)=−ν∂v∂x|x=0+gβ∫0δ(y)(T−T∞)dx \frac{d}{dy}\left( \int_{0}^{\delta(y)} v^{2} dx\right) = -\nu \left. \frac{ \partial v }{ \partial x } \right|_{x=0} + g \beta \int_{0}^{\delta(y)} (T-T_{\infty}) dx

ddy(∫0δ(y)v(T−T0)dx)=−α∂T∂x|x=0 \frac{d}{dy} \left( \int_{0}^{\delta(y)}v (T-T_{0}) dx \right) = -\alpha \left. \frac{ \partial T }{ \partial x } \right|_{x=0}

with T−T0=(Tw−T0)(1−xδ)2T-T_{0}=(T_{w}-T_{0}) \left( 1-\frac{x}{\delta} \right)^{2} , v=v0xδ(1−xδ)2v=v_{0} \frac{x}{\delta} \left (1-\frac{x}{\delta}\right)^{2} and T0=T00+γyT_{0}=T_{00}+\gamma y

  1. Derive the integral momentum and energy equations in terms of the following non-dimensional parameters

δ*=δHRaH−1/4y*=yHv*=vαHRaH1/2RaH=gβ(Tw−T00)H3ανb=γHTw−T00 \begin{align} \delta* = \frac{\delta}{H Ra_{H}^{-1/4}} & & y* = \frac{y}{H} \\ v* = \frac{v}{\frac{\alpha}{H}Ra_{H}^{1/2}} & & Ra_{H}= \frac{g \beta (T_{w}-T_{00})H^{3}}{\alpha \nu} \\ b = \frac{\gamma H}{T_{w}-T_{00}} \end{align}

  1. Solve these equations in the limit of Pr→∞Pr\to \infty by setting b→1b\to1

  2. Compare your estimate with the literature (Nu¯=0.337RaL1/4\overline{Nu}=0.337 Ra_{L}^{1/4})

Solution

Cooling a bottle - horizontal or vertical?

You have a bottle of water at room temperature, and you would like to drink it cold as soon as possible. The bottle has a height/diameter ratio of about 5. You place the bottle in the refrigerator; however, you have the option of positioning the bottle (1) vertically or (2) horizontally. The refrigerator cools by natural convection (it does not employ forced circulation). Which way should you position the bottle? Describe the goodness of your decision by calculating the ratio h1/h2h_{1} / h_{2}, where hh refers to the heat transfer coefficient.

Solution

Effect of orientation on heat transfer from flat plates

A long, rectangular metallic blade has width H= 4 cm and temperature Tw = 400C. It is surrounded on both sides by atmospheric air at T∞_{\infty}= 200C. The long side of the blade is always horizontal. Calculate the total heat transfer rate per unit of blade length when the short side of its rectangular shape (H) is (a) vertical, (b) inclined at 450 relative to the vertical, and (c) horizontal. Comment on the effect that blade orientation has on the total heat transfer rate.

Solution

Heat transfer from horizontal cylinders

An electrical wire of diameter D= 1 mm is suspended horizontally in air of temperature 200C. The Joule heating of the wire is responsible for the heat generation rate q’= 0.01 W/cm per unit length in the axial direction. The wire can be modeled as a cylinder with isothermal surface. Sufficiently far from the wire, the ambient air is motionless. Calculate the temperature difference that is established between the wire and the ambient air. (Note: This calculation requires a trial-and-error procedure; expect a relatively small Rayleigh number.)

Solution

Effect of wall thickness on the validity of isothermal wall assumption

In many analyses of natural convection heat transfer problems, the vertical wall heating a fluid or dividing two differentially heated fluids is modeled as isothermal. This is an approximation valid in some cases and invalid in others. To be isothermal, while bathed by natural convection in boundary layer flow, a vertical solid wall must be thick enough. Comparing the thermal conductance to vertical conduction through the wall (kwW/Hk_{w} W / H) with the thermal conductance to lateral heat transfer through the same wall (and the fluid boundary layer, kH/δTkH / \delta_{T}, determine below what range of wall widths, WW, the ‘’isothermal wall’’ assumption becomes inadequate (kw,H,k,δTk_{w},H,k,\delta_{T} are the wall thermal conductivity, wall height, fluid thermal conductivity, and thermal boundary layer thickness, respectively). For a wall of fixed geometry (W,HW,H), is the isothermal wall assumption getting better or worse as RaHRa_{H} increases?

Solution

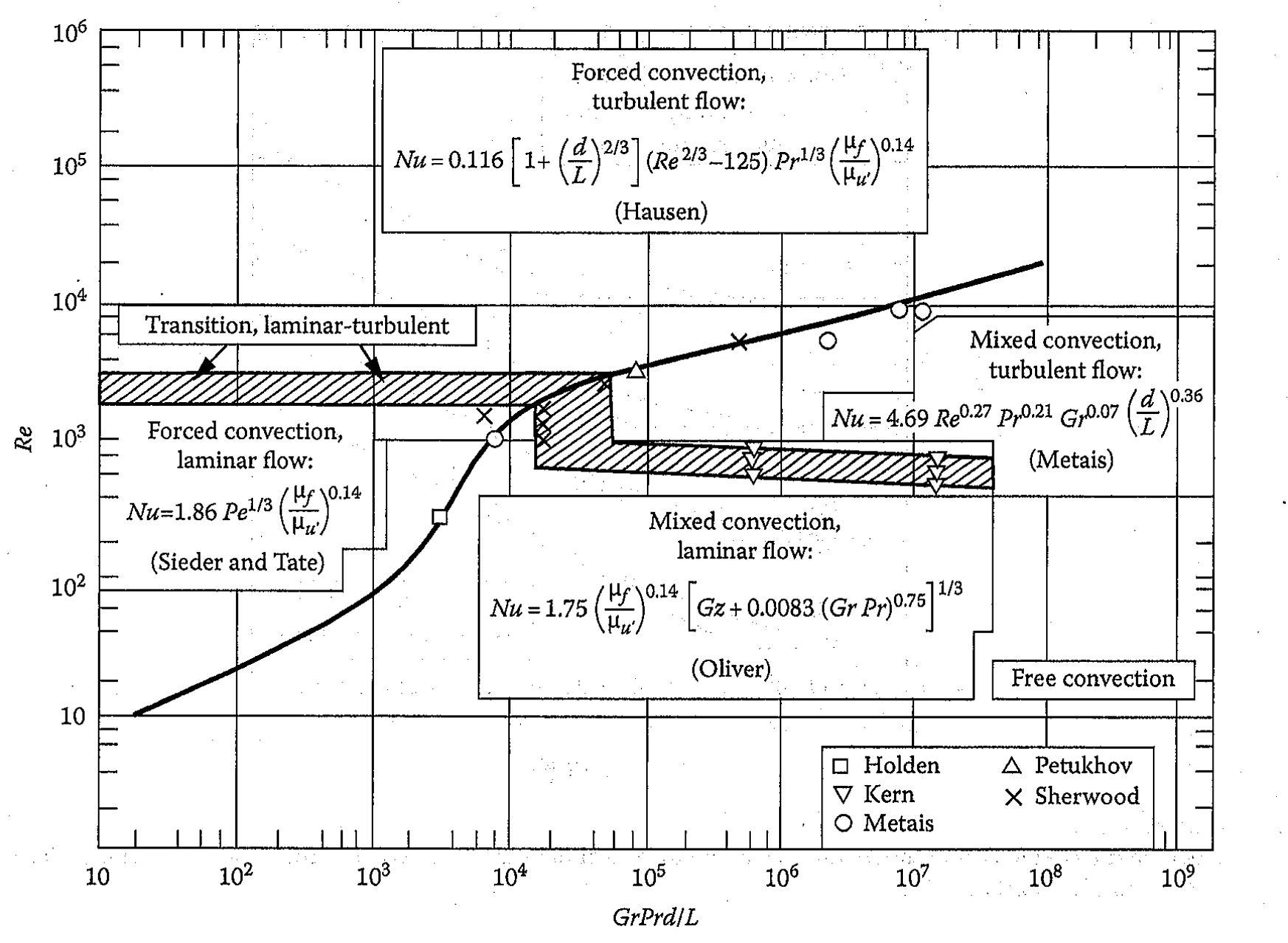
Heat Transfer Calculation in Mixed Convection

Air at atmospheric pressure and 20°C is forced through a horizontal 1 in. diameter tube at an average velocity at 0.3 m/s. Tube wall is maintained at a constant temperature of 140°C. Calculate the heat-transfer coefficient for this situation if tube is 12 in. long. (For correlations refer Figure 2)

Solution

Heat Transfer in an enclosure between two parallel plates

Air at atmospheric pressure is enclosed between two vertical plates of length 1m each separated by 2 cm. The temperatures of the plates are 60°C and 100°C, respectively. Calculate the heat flux across the space. (use appropriate correlations from the slides)

Solution

Thank You

Go to Home